Outline for
Introduction to the Practice of Statistics
by David S. Moore and George P. McCabe
- Chapter 1: 1.1,
1.2, 1.3
- Chapter 2: 2.1,
2.2, 2.3,
2.4, 2.5,
2.6, 2.7
- Chapter 3: 3.1,
3.2, 3.3,
3.4
- Chapter 4: 4.1,
4.2, 4.3,
4.4, 4.5
- Chapter 5: 5.1,
5.2, 5.3
- Chapter 6: 6.1,
6.2, 6.3,
6.4
- Chapter 7: 7.1,
7.2, 7.3
- Chapter 8: 8.1,
8.2
- Chapter 9
- Chapter 12
- Chapter 13
Chapter 1
What is statistics?
Section 1.1
- Important questions of statistics
- What questions are relevant to the data?
- Who are the individuals the data describes?
- What, precisely, are the variables?
- How was the data acquired?
- How can the information in a single variable
be described succinctly?
- Are there relationships between variables?
- Exploring (single) variables
- Use of graphs, charts, stem plots, histograms?
time plots (Q: Can each of
these be used equally well for all types of variables?)
- Features of note: center, spread, deviations, symmetry,
number of modes, outliers, seasonal variation, trends
(Q: Do each of the aforementioned
concepts apply to all types of variables?)
Terms to Know: statistics, individuals, cases,
variable (categorical and quantitative), frequency and
relative frequency, distribution, bar graph vs. histogram
(what is the difference?)
Section 1.2
- Numerical summaries of distributions
- Why do we use them?
- What are the the drawbacks of their use?
- For what types of distributions are they most
effective (Note: the answer may not be the
same for all numerical summaries!)
- Which are resistant?
- Which measures of center and spread are paired together?
- Outliers
- Be able to recognize them (from graph — See Sect 1.1;
1.5 × IQR method)
- Propose appropriate (context-specific) ways of
dealing with them
Use of Technology: Be able to
- Enter data
- Sort data
- Find the mean, median, variance, standard deviation
- Produce box plot (Minitab only)
Terms to Know: mean, median, measure of center/spread,
resistant measure, percentiles/quartiles, IQR, five-number summary,
box plot, linear transformation
Section 1.3
- Density curves
- How can a smooth curve represent a distribution?
- Why is this type of “mathematical model”
useful?
- Why is it essential that the area under such a
curve be 1?
- Describe the placement of mean, median
and percentiles along such a curve
- What is special about “normal” (density)
curves? How many such curves are there?
- Normal distributions
- How do you tell if a distribution is well-approximated
as a normal distribution?
- What are some types of data which are typically
normally distributed?
- Standardizing a normal distribution
- Amounts to a linear transformation
- Computing
z-scores and going
from such a standardized score back
to an unstandardized one
- Use of Table A to determine
area under the standard normal curve,
and interpreting the meaning of such areas
- Why standardize?
-
Normal probabilities
Use of Technology: Be able to
- answer questions such as those posed in Examples
1.25-1.27
- produce normal quantile plots for a given set of
data (Minitab only)
- perform density estimation for a given data set
(Minitab only)
Terms to Know: density curve, normal curve,
(standard) normal distribution, standardized value (or
z-score), normal quantile plot (normal probability
plot), granularity
Chapter 2: Looking at Data —
Relationships
- Association between variables
- Describe tendencies, not hard-and-fast rules
- Not same as causation
- Explanatory variable(s)
- Often chosen as a result of how data is to be used
- Even if data suggests association, wrong to assume
changes in explanatory variable cause changes
in response variable
- Guiding principles
- Start with graphical analysis, then add numerical
summaries
- Look for overall patterns and deviations from
those patterns
- When the overall pattern is quite regular, use a compact
mathematical model to describe it
Terms to Know: associated variables,
explanatory/response variables, causation
Section 2.1: Scatterplots
- Scatterplots
- Relationship between two quantitative variables
- Each individual in the study has corresponding point
- If one variable designated as explanatory, put it on
horizontal axis
- Including a categorical variable as a 3rd variable
- Examining scatterplots
- Look for the overall pattern in the graph, and for
striking deviations from that pattern
- Describe the overall pattern by the form, direction
and strength of the relationship
- Keep an eye out for outliers, noticeable deviations
from the overall pattern
- Avoid quick judgment, even with strong overall
pattern, until you consider lurking variables
- Studying relationships between a categorical variable
and a quantitative one
- Use methods of Chapter 1 (back-to-back stemplots,
side-by-side boxplots, etc.)
- Cannot discuss positive/negative relationship except
in those cases where categorical variable has
natural ordering (See Example 8, p 115)
Terms to Know: scatterplot, overall pattern,
deviation from a pattern, form/direction/strength of a
relationship, outlier, positive/negative association, linear
relationship, cluster, smoothing a scatterplot
Section 2.2: Correlation
- Correlation
- Establishes the strength of a linear relationship
between two quantitative variables
- Properties
- r has same value regardless of which variable
is considered explanatory
- Direction of relationship comes from sign of r
- r has no units, and is unaffected by which
units are used for a variable
- -1 £ r
£ 1
- Will not detect strong nonlinear relationships
between variables (Plot your data!)
- Not resistant to outliers
- Understand the formula as one involving standardized
scores for the two variables
- Determining r values by sight
- Changes in scale do not affect correlation, but
can make our eyes think so
-
Practice determining r ; or see a scatterplot
for a given value of r
Terms to Know: linear relationship,
correlation, strength of a relationship
Section 2.3: Least-Squares Regression
- Least-squares regression line
- Requires two quantitative variables, one designated as
explanatory (x), the other as response (y)
- The line that best fits the data (i.e., of all possible
lines drawn, it's the one that makes the sum of squares
of vertical distances to data points the smallest)
- Calculation of slope, y-intercept from data (p. 141)
- Is dependent upon the units of measurement for
explanatory/response variables
- Prediction
- Regression line is used to predict value of response variable
y at a fixed value of explanatory variable x
- Reliability/accuracy
- Interpolation (prediction at x value falling inside
observed data values) vs. extrapolation (prediction at x
values far from observed values; often inaccurate)
- Interpolated values should be good if strength of fit
is good (i.e., if r2 is close to 1 —
see below)
- Poor results may occur if regression line in one population
is used to make predictions in another population
- Connections between correlation and regression
- Correlation used in calculation of slope for regression line
- r2 = (variance of predicted values)/(variance
of observed values); i.e., it is the fraction of variation in
response values that is explained by least-squares regression
of y on x
Terms to Know: regression line, slope, intercept,
prediction, square of the correlation
Section 2.4: Cautions about Correlation
and Regression
- Assessing strength of a linear relationship
- Look at residuals
- Difference of observed value and predicted (by
the regression line) value
- Part of the variation in the response variable
left unexplained by the linear association
- Mean of residuals for least-squares regression
is always 0
- Residual plots
- Scatterplot with unchanged explanatory variable,
but response variable is the residual
- Can support or refute whether overall pattern
of original variables is linear (see discussion
of Figure 2.19 on p. 156)
- Looking beyond regression
- Time plot of residuals — one way presence of
lurking variable may be detected
- Investigating outliers (both in x and
y directions
- Large studentized residuals help to detect outliers
- Large DFITS help to detect influential observations
- Warnings
- Beware lurking variables
- Do not take associations as causation
- Correlations based on averaged data are likely to be
much stronger than with individual observations
- Successful prediction does not require a cause-and-effect
relationship
Terms to Know: residual, residual plot,
outliers, influential points, restricted-range
Section 2.5: An Application — Exponential
Growth and World Oil Production
Section 2.6: Relations in Categorical Data
- Distributions of a two-way table
- Marginal distributions
- Conditional distributions
- At the cell level
- Involves looking at row/column percents
- Key to discovering nature of relationship between variables
- That some relationship exists can be ascertained using
test of significance of Chapter 9
- Column/row percents can be plotted in histogram
- Simpson's paradox
Illustrates how aggregate data can hide lurking variables
Terms to Know: counts/frequencies,
percents/relative frequencies, two-way table, row/column variable,
marginal distributions, conditional distributions, three-way
table, aggregate data
Section 2.7: The Question of Causation
- Explanations for associations
- Direct causation
- Direct cause-and-effect between explanatory and
response variables
- Difficult to prove via an observational study; best
established through controlled experiments
- Common response
Both explanatory and response variables change in response
to some third (lurking) variable
- Confounding
- Lurking variable(s) present
- Cannot distinguish between effects of several variables
upon the response variable
- Evidence for causation outside of a controlled experiment
- Association is very strong
- Association is consistent across numerous studies
- Higher levels of treatment associated with stronger
responses
- Alleged cause preceded (in time) the response
- Alleged cause is plausible
Terms to Know: cause-and-effect, lurking
variables, common response, confounding
Chapter 3
Understand the difference in attitudes when looking at data for:
- exploratory data analysis
- an answer to a specfic question
Section 3.1
- Some Internet resources of (available) data
- Designs for producing data
- Sampling
What are the advantages/disadvantages as compared
to a census?
- Observational studies vs. experiments
- What types of questions can/cannot be answered using
an observational study? (see also Section 3.2)
- Be able to give examples of each type.
Terms to Know: anecdotal evidence, available data,
designs, sample, census, observational study, experiment,
confounding
Section 3.2
- Advantages of experiments (over observational studies):
- Provide good evidence for causation
- Can minimize the effect of lurking variables
- Can study effects of combined factors
- Design of experiments
- Control
- Comparisons between treatments
- Arranging experimental units (subjects) into blocks
- Compare to “strata” for sampling
- Matched pairs (only when there are just
two treatments)
- Randomization
- Purpose: to remove effects of lurking variables
- Complete vs. randomization within blocks
- Use of Minitab and Table B to randomize
- Replication (many experimental units reduce effects of
chance variation
Terms to Know: experimental units/subjects, treatment,
factors, explanatory/response/lurking variables, level, placebo,
placebo effect, causation, bias, control/experimental group,
matching, randomization, statistical significance,
blind/double-blind study, lack of realism, blocks
Section 3.3
- Some designs for sampling
- Voluntary response samples
- Ex: A TV news magazine gives an 800-number for
the audience to express its opinion.
- Highly subject to bias
- Probability samples
- Each member of the population is assigned a certain
probability for being chosen and random chance is
used to choose
- SRS is special case whem each member of population
is assigned the same probability (i.e., equally-likely
to be chosen)
- Stratified random samples
- Population is divided into “strata”
(analogous to “blocks” from experiments)
- An SRS is taken within each stratum
- Mulstistage samples
- A hybrid of stratifying and using SRS
- Population is stratified (or subdivided)
- SRS used to select subdivisions to work wth
- Makes “door-to-door” interviews more
practical (less costly)
- Issues surrounding surveys (and statistical studies in general)
- Questions to ask in determining the
soundness of a statistical study
- Given the answers to the above list of questions, what
types of bias is the study prone to?
Terms to Know: population, sample, undercoverage,
nonresponse/response bias
Section 3.4
- Simulations
- Understand how simulations give a sense of the
amount of variability in a statistic for various
sample sizes.
- Be able to use Minitab to produce a sampling
distribution (such as Fig. 3.6) when given:
- sample size
- actual value of parameter p
- Questions:
- If the sampling proportion of an SRS is an “unbiased
estimator”, what would an example of a “biased
estimator” look like?
- In Example 3.22 we saw that 95% of the time an SRS of
sample size 2500 comes within 2% of the actual parameter
value 0.6. Is this true if the sample size is the same
as the size of the population (i.e., a census)?
Why or why not?
- Just how can, in the words of the authors on p. 275,
“the true distance of a statistic from the
parameter it is estimating ... be much larger than
the sampling distribution suggests”?
Terms to Know:
parameter, statistic, sampling variablility, simulation,
sampling distribution, unbiased estimator, capture-recapture
sampling
Chapter 4
Section 4.1
- Definition of probability
- Empirical (probability = long-term relative frequency)
- Relies entirely on randomness
- Short-term results are unpredictable
- Long-term pattern behavior
- Independence of trials
- Fundamental nature of the assumption
Q: Is probability theory anti-religion?
- Difficult for people to accept
- Law of Averages (the gambler's
fallacy): “I just got
10 heads in a row; must be due
for some tails.”
- Myth of short-run regularity:
“I made 10 shots in a row; must
have the touch tonight.”
Terms to Know: random, probability
(empirical vs. intuitive — see Section 4.2,
p. 297, for the latter)
Section 4.2
- Probability Model (Note the connection to
sampling distribution)
- List of all possible outcomes (sample space )
- Assignment of a probability to each outcome
- 0 £ P(A)
£ 1 for every
event A
Note how probabilities are assigned under
the assumption that the finitely-many
outcomes are equally-likely.
- If S denotes the sample space, then
P(S) = 1
- P(A C ) = 1 - P(A) for
every event A
- Sum rule: P(A or B) = P(A) + P(B)
- Requires events A and B
to be disjoint (use of Venn diagram
to determine this)
- P(A) = å
P(Ai ) , where the
Ai are the
(finitely-many) individual
outcomes in event A
- See Section 4.5 for more general sum rule
(one that applies even for non-disjoint events)
- Computing probabilities using multiplication rule:
P(A and B ) = P(A) P(B)
- Events A and B must be independent
- Different concept from disjointness
- Independence cannot be determined from Venn
diagram (unlike disjointness)
- See Section 4.5 for more general multiplication rule
(one that applies even for non-independent events)
Terms to Know: probability model, outcome,
sample space, event, disjoint events, independent events,
complement of an event, addition (sum)/multiplication rule
Section 4.3
- Discrete random variable
- A certain kind of probability model
- Lends itself well to display via a probability
histogram. Some have special names:
- Figure 4.6(a) (probability of obtaining
a certain digit from a table of random
digits) is example of a uniform
probability distribution
- Figure 4.8 (Example 4.16) is an example
of a binomial probability
distribution
- Continuous random variable
- Probability model is specified by a density curve
- Probability of an event corresponds to an
area under the curve. Note the implications
of P(S) = 1 .
- Individual outcomes have probability 0.
Thus P(X < v) and P(X
£ v) are
equal.
- Important class of examples are the
normally-distributed continuous random
variables
Terms to Know: (discrete/continuous)
random variable, density curve, probability histogram
Section 4.4
- Summarizing probability distributions
- Mean (expected value)
mX of a random
variable X
- Know how to calculate for discrete random
variables (use weighted average)
- Law of Large Numbers and estimation of
m
- Variance/standard deviation for a discrete random
variable
- Rules for means, variances
- under linear tranformation: a + bX
- of the sum of two random variables (Note the
independence requirement for variances)
- Law of Large Numbers
- Allows stable prediction of random outcomes
- Does not tell how large
- Contrast to the various “laws of small
numbers ” on p. 332 — randomness
is generally misunderstood by the public
Terms to Know: weighted average,
mean/variance/standard deviation of
a probability distribution (mean = expected value),
Law of Large Numbers
Section 4.5
- Conditional probability
- Events need not be independent
- Q: What does P(B | A ) equal
when A and B are independent?
- Expanded rules for computing probabilities
- Addition Rule (Inclusion-Exclusion Principle):
P(A or B ) = P(A) + P(B) - P(A
and B )
- Multiplication Rule: P(A and B) = P(A)
P(B | A )
- Combinations of these rules and use of
tree diagrams
- Bayes' Rule
Terms to Know: union, intersection,
conditional probability, personal probability
Chapter 5
Section 5.1
- Binomial Distributions
- A discrete probability distribution
- Applicable situations (i.e., binomial
settings)
- n (a fixed number) independent
observations (rule-of-thumb:
population-to-sample size ratio
at least ten is sufficient for
approximate independence; see
Example 5.3 and following)
- Each observation falls into one of
two categories (call them successes
and failures)
- Probability of success is p (fixed)
for each observation
- A different binomial distribution B(n, p)
for each pair of values n and p
- Skewed for small values of n,
p
-
Approximately normal when np ³ 10
and n(1 - p)
³ 10 (that is, when
the expected number of successes and
failures are both at least 10)
- Computing probabilities for binomially-distributed
random variables
- Table C
- Using calculator/Minitab
- Formulas for mean, standard deviation of
B(n, p) (bottom, p. 380)
- Count vs sample proportion
- Both are natural random variables for
categorical outcomes
- proportion = (count)/(number of observations)
- Mean and standard deviation formulas for proportion
- Valid if count is binomially distributed;
approx. valid in SRS where population-to-sample
size ratio is at least 10
- Mean formula shows sample proportion for
an SRS is unbiased estimator of parameter
p
- S.D. formula quantifies how spread goes
down as sample size goes up
- Probability distribution of sample proportion
- Not binomially distributed even when count is
- Like count, it is approximately normal
when np ³
10 and n(1 - p) ³ 10
- Approximating binomially-distributed random variable
with normal distribution
- As a rule, do only if np
³ 10 and n(1 - p) ³ 10
- Expect better results if p » 1/2
- Use continuity correction when n
is not large
- Binomial probabilities P(X = k)
- Found in Table C for certain values of n ,
k and p
- Formula from which these table values come
(see p. 388)
Terms to Know: population vs.
sampling distribution (related to parameter
vs. statistic ), sample proportion,
binomial distribution, count, continuity correction,
success/failure, factorial, unbiased estimator (p. 382)
Section 5.2: Sampling Distribution of Sample Mean
- Sample mean in an SRS of size n
- A random variable X
- Individual observations Xi
also random variables
- Each Xi distributed as the population, if
population is large compared to size n of sample
- Mean and S.D. for each Xi is population
mean and S.D.:m and
s
- Definition of X: X = (1/n)
S Xi
- Mean and standard deviation of X — see p. 399
-
Distribution of mean X compared to population
distribution
- Distribution of X is
- normal if population (individual Xi )
is normal
- increasingly normal (as sample size n increases)
even if population is not (Central Limit Theorem)
- Spread for X not as great as for population; decreases as
n increases (reflected in formula for S.D.)
Terms to Know: sampling distribution, sample
mean, unbiased estimator
Section 5.3
Chapter 6: Inference on the mean
Section 6.1: Confidence intervals
- Nature of confidence intervals
- Range from (estimate - margin of error)
to (estimate + margin of error)
- Have an associated confidence level C
- C percent of the time the confidence
interval for the estimated statistic
contains the parameter — see
Fig. 6.2, p. 438
- Desirable to have C as high as possible
(usual values: 90%, 95%, 97%)
- Margin of error
- Desirable to have as small as possible
(at odds with desire for large
confidence interval)
- Can decrease in one of three ways
(see bullets on p. 442)
- Assume unbiased estimator of parameter —
account only for chance variation
- Confidence interval for a population mean
- Underlying assumptions
- Population is normally distributed
- Without this, confidence won't be as great
as advertised
- With n ³
15 (# of observations), no extreme
outliers or skewness confidence
isn't severely compromised
- Data is unbiased, subject only to
random sampling error
- Data is an SRS of the population, or can be
considered as one (not a
multistage/stratified sample)
- Extends from (sample mean - margin of error)
to (sample mean + margin of error)
- The “fine print”
- If possible, explain and/or correct
outliers (nonresistance of sample mean)
- In practice, won't know
s; might substitute sample standard
deviation s if large sample size
- Mustn't interpret
- confidence level as a probability that true
mean lies in interval; rather, as how often
the method gives correct answers
- confidence interval/level as a
prediction that C% of observations
lie inside this interval
Terms to Know: margin of error,
inference, confidence level
Section 6.2: Significance Tests
- Hypotheses
- Null hypothesis (H0 )
- A supposition about a population parameter: p
= p0 (in this section,
m = m0)
- Will test compatability of H0
with sample statistic
- Alternative hypothesis (Ha )
- Statement of an alternative to H0
we suspect to be true
- One-sided (Ha: p > p0 or
Ha: p < p0 ) vs. two-sided
(Ha: p ¹
p0 )
- Test for mean
- Underlying assumption: sample mean is
normally-distributed as N(m,
s/Ön )
- True if population is normally distributed
- Approximately true if sample size n is large
- Compute test statistic (a z-score) for sample
mean assuming hypothesized population mean
- Get associated P-value (probability associated with
test statistic and Ha ; see box, p. 461)
- Compare P-value to predetermined significance
level a
- a is a percentage
(i.e., it is between 0 and 1)
- Common levels of significance: 0.1, 0.05, 0.01
Terms to Know: null hypothesis,
alternative hypothesis (1 or 2-sided), test
statistic, P-value, statistical significance
Section 6.3: Use/Abuse of Tests
- Significance tests are not appropriate for all data sets
- Outliers can exaggerate/de-emphasize significance
- Confounding is not removed by such tests
- Statistical significance establishes results are
unlikely due to random chance
- Does not provide reason for significance (could
be some suspected effect of a treatment, could be
poor study design)
- Significance level a
- Importance of choosing a level ahead of time when
decisions will be made based upon results
- Choosing a level: Consider
- how believable is the null hypothesis
- consequences of rejecting null hypothesis
- Avoid thinking of results as insignificant if a not reached, significant
if it is
- Misinterpreting statistical significance
- Statistical significance vs. practical importance
- Significance may lead to rejecting null hypothesis in
favor of alternative; lack of significance only means
results are consistent with null hypothesis
- Danger of “searching for significance”
Section 6.4
Chapter 7
Section 7.1: Inference for the Mean of
a Population
- t distributions
- Correct distribution for sample mean when
s (for underlying
population) is not known and s (the
sample standard deviation) is used in its
place
- Description
- Standardized so centered about 0
- Symmetric and bell-shaped
- Larger spread than normal distribution
- Degrees of freedom
- df = n - 1
-
More like N(0, 1) as df increases
- One-sample t confidence intervals
- Used in place of confidence interval for population
mean (as learned in Section 6.1)
when s (for population)
is unknown
- Determination of margin of error
- One-sample t statistic (determined for a confidence
level C from Table D) used in place of
z statistic
- Use standard error of sample mean in place of standard
deviation for sample mean
- One-sample t test
- Used in place of z test (see Section
6.2, p. 461) when s unknown
- Formulate null/alternative hypotheses just as usual
- Determine t statistic as you would z
statistic, but using SE for sample mean rather than
SD
- Determine P-value from appropriate t
distribution (Table D)
- Note method of reporting conclusion (as at end of
Example 7.5, p. 511)
- Matched pairs t procedures (comparative
inference)
- Procedures are just like above, but performed on
the difference
- Usually have H0 :
m = 0 and one-sided alternative
hypothesis
- When are t procedures valid
- Exactly correct when population is normal
- Approximately correct when n
³ 15 except in case of outliers or
strong skewness
- Clear skewness (no outliers) OK if n ³ 40
- Power of the t test
This is optional reading. To fully understand the discussion,
you ought to study Section 6.4 as well.
- Inference for non-normal populations
- Use a known distribution that is not normal but fits well
- Make a transformation that brings about normality
- Use distribution-free procedures (Example: the sign test
Terms to Know: standard error, one-sample
t, degrees of freedom, matched pairs test, robust
Section 7.2: Comparison of Two Means
- Context of two-sample problems
- Want to compare responses in two groups
- Often (but not exclusively) used in comparative experiments
- Usually comparisons made on groups mean responses
- Groups can be considered as samples from distinct
populations
- Responses of units in one group independent of those in
the other
- Two-sample statistics
- Two-sample z statistic
- How the formula follows from previous (one-sample)
z statistics
- Two random variables, one from each group (measuring same
thing, but possibly having different distributions)
- Looking at difference between these variables, so
sample/population mean is difference of ones for each
group, variance for difference computed from individual
variances via formula, p. 337
- Is distributed normally (or approximately so) as N(0, 1)
when underlying populations are normal (or approximately)
- Used when standard deviations for underlying populations
are known (somewhat unusual)
- Two-sample t statistic
- Used when
- Samples and population distributions of both groups
satisfy conditions mentioned in Section
7.1 for t procedure validity, and
- standard deviations of populations are not known
- Formula is one arising naturally from that for two-sample
z statistic
- Does not have t distribution
- Is approximately t for the correct df
- Best df comes from formula, p. 549 (but use
software or method below instead of memorizing this)
- We get good (conservative) estimate taking
df = min{n1 - 1, n2
- 1 }
- Inference on the difference of two population means
- Two-sample t significance test
- Null hypothesis: the population means are equal
- Notation used in results
- Interpretation of results
- Two-sample t confidence interval
Interpretation of such an interval
- Robustness
- Most robust against nonnormality if sample sizes equal
- If sample sizes equal and distributions of two populations
the same, can take sample sizes as low as 5
- Using t procedures with small samples
- Optional material
- Software approximation for degrees of freedom
- Pooled two-sample t procedures
Terms to Know: difference of sample means,
two-sample z and t statistics, conservative
estimates
Section 7.3: Optional Topics in
Comparing Distributions
Chapter 8
Section 8.1: Inference for
1-proportions
- Large-sample confidence interval for population
proportion
- Basic assumptions
- Population-to-sample size ratio
is at least 10 (so count is
approximately binomially distributed)
- Sample size is large enough that expected value of
successes and failures are both at least 10 (so
binomial dist. well-approximated by normal dist.)
- Interval is (
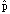 - m,
- m, 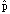 + m )
+ m )
- Margin of error determined differently
than for inference on a population mean
(see Section 6.1)
- Standard error (SE) of sample proportion:
like standard deviation with sample
proportion in place of true proportion
(unknown parameter)
- Desired level of confidence (percentage)
®
z* (from
¥ row of Table D)
- Large-sample significance test for population proportion
(H0 : p = p0 )
- Comparison to confidence interval
- Significance test good if specific (ideal)
p0 is suspected
- Confidence interval provides range of
compatible p
- Basic assumptions: as for confidence intervals
but np0
³ 10 and n(1 - p0 )
³ 10.
- P -values determined from appropriate choice of
P(Z £ z ) ,
P(Z ³ z ) or
P(Z ³ |
z | )
- Determination of sample size
Must first specify:
- a desired margin of error m
- a desired level (percentage) of confidence ® z*
- a guessed p* at
the true proportion (can take worst-case
guess p* = 0.5 )
Terms to Know: standard error,
approximate level C confidence interval,
null/alternative hypothesis, P -value,
z-statistic (test statistic), sample proportion
Section 8.2: Comparison of
Two Proportions
- Setting
- Have categorical data (one variable, 2 options)
for samples from two groups (populations)
- Want to compare proportions between populations
- Inference procedures on the difference of two population
proportions (Interpretation and notation)
- Confidence intervals
- Tests of significance
- Standard error arrived at in a somewhat different
way than all previous standard errors
- pooled estimate (combining of two sample proportions)
- Null hypothesis: the two population proportions are equal
- Optional material
Relative risk
Terms to Know: difference of sample proportions,
pooled estimate
Chapter 9: Inference for Two-Way Tables
- Two-way tables
- Give counts for two categorical variables
- Can be used for categorical information (S or F) for
samples from 2 populations (like material studied
in Section 8.2)
- Variables may have more than two options, resulting
in more rows and/or columns
- Constructing them
- Columns for explanatory variable, rows for response variables
- Additional row/column for totals
- Grand total
- Row/column/marginal percents
- Test of significance
- Results in 2 ´ 2 case
same as if you use procedures of Section
8.2
- Hypotheses
- Null hypothesis: No association between variables
- Leads to expected cell counts
- Rejected for small P-value (taken from Table
F; see below) in favor of alternative hypothesis
- Alternative hypothesis: association exists
- Always two-sided
- Exact nature of association ascertained by
looking at data and should be included in answer
(see, for example, the 1st paragraph on p. 632;
the last full paragraph on p. 636)
- chi-square statistic
- df = (#rows - 1)(#cols - 1)
- Distributed as
c 2(df) (Table F) if
- table is 2 ´ 2
and each expected cell count is at least 5
- table is bigger than 2
´ 2, each
expected cell count is at least 1, average
expected cell count is at least 5
- Two models for two-way tables (neither of which would
be open to including the same unit in counts appearing
in different cells)
- Explanatory variable is the population (i.e., each
column represents a different population — as
in male vs. female; GM cars vs. Ford vs. Chrysler)
- Columns represent subdivisions within a single
population (as in categorizing Americans by their
age as in Table 4.1, p. 350; cats by their source
as in Exercise 9.3, p. 644; etc.)
- Optional material
Meta-analysis
Terms to Know: two-way table, cell,
row/column percentages, expected cell counts,
chi-square statistic, joint/conditional distributions
- Setting for its usage
- Two variables: one categorical, one quantitative
- Categorical variable usually is population (group)
to which unit belongs
- Extension of idea, called two-way
ANOVA, can deal with two categorical, one
quantitative variable
- Extension of 2-sample t test
- Comparison of means (of quantitative variable)
between groups
- Gives same results as 2-sample t test
when just two groups
- The model assumptions
- There are I populations
- A sample is drawn from each population
- Sample size from 1st population is
N1, from 2 population is
N2, etc.
- xij represents the
jth observation from
the ith group
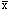 i
represents the sample mean (statistic) within the
ith group
i
represents the sample mean (statistic) within the
ith group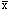 represents the sample mean (statistic) for all
observations in all groups
represents the sample mean (statistic) for all
observations in all groups
- Each population is normally distributed about a mean
mi
with standard deviation
si
(parameters)
Assumption should be checked when possible by
looking at histograms/normal quantile plots within
each group
- Each si
is the same (i.e.,
si =
s for each i )
- If not, the problem can often (but not always)
be overcome with a transform of the data
- Not usually worth formal test to see if S.D.s
are the same — consider OK if rule in
box on middle of p. 752 is satisfied
- Estimate s
using pooled (sample) standard deviation
sp (sp2
= MSE in Minitab output; see formula on
bottom of p. 752)
- One-way ANOVA test
- A test of significance
- H0: "no difference in mean between
groups"
- Ha: mean in at least one group
differs from other groups
- Test statistic
- F statistic
- F = MSG/MSE
- Use of dfs in computing MSG/MSE from
SSG/SSE
- Degrees of freedom in numerator:
DFG = I - 1
- Degrees of freedom in denominator: DFE =
N - I (N is total number
of units across all groups)
- Gives ratio of variation among group means
to variation within groups
- New distribution, called an F distribution
- Table E in back of text
- Requires knowledge of F statistic, df
for numerator (DFG), df for denominator (DFE)
- Coefficient of determination R2 =
SSG/SST. (Like in regression, indicates
percentage of total variation in means from samples are
explained by population)
- If test demonstrates significance, further analysis
must be done to determine how means vary
between groups; some alternatives:
- Graphical displays (side-by-side boxplots,
histograms, etc.)
- Contrasts
- Preferable when investigator has predisposed
opinion about how means will compare in
various groups
- We will not study these
- Multiple comparisons
- Inspect difference of means between any two
groups (idea is like, though not the same as,
using a 2-sample t test on each possible
pairing of groups)
- Tests of significance are possible on differences
of these means — we will not do
- Confidence intervals on pairs of differences of
means: Be able to
- understand/interpret Minitab output
for Tuckey's/Fisher's Pairwise Comparisons
- understand why the difference in individual
and overall (or family ) error
rates
Terms to Know: one-way ANOVA, group,
variation among/within groups, ANOVA table, degrees
of freedom (DFG, DFE, DFT), sum of squares (SSG, SSE,
SST), mean squares (MSG, MSE), F statistic,
multiple comparisons, coefficient of determination
(R2), pooled standard deviation
(sp)
Chapter 13: Two-Way ANOVA
Terms to Know:
Last Modified:
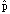 - m,
- m, 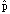 + m )
+ m )